In polar coordinates,
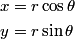 and 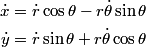 so, the kinetic energy 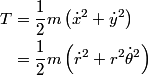 The potential energy is 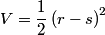 So, the Lagrangian is 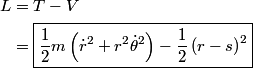 Therefore, answer (D) is correct. |
In polar coordinates,
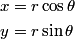 and 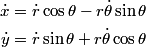 so, the kinetic energy 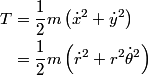 The potential energy is 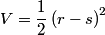 So, the Lagrangian is 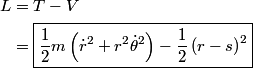 Therefore, answer (D) is correct. |